Une théorie plus grande de la conception des systèmes : ce qui ne va pas avec la modernité et la post-modernité, comment survivre à l'avalanche à venir, et comment résoudre les principaux problèmes auxquels nous sommes confrontés. Première partie : Les systèmes sont des modèles. Mais qu'est-ce qu'un modèle ?

Je promets que cela deviendra pratique à un moment donné, mais d'abord, nous devons poser quelques bases. Si vous trouvez les bases évidentes ou si vous êtes prêt à me croire sur parole, n'hésitez pas à les sauter. Mais en fin de compte, sans ce contexte, vous ne pouvez même pas vraiment comprendre la proposition.

Sans perte de généralité, tout système peut être considéré comme un graphe de paramètres connecté par des arêtes, où les nœuds sensoriels reçoivent des entrées qui entraînent à la fois des changements internes du graphe et produisent des sorties aux nœuds actifs.

Un modèle est un système qui agit pour minimiser l'erreur de prédiction par rapport aux prioris incarnés par son graphe de paramètres.

Les systèmes sont toujours des modèles car les systèmes doivent continuer à persister, et s'ils prennent des actions incompatibles avec les conditions de persistance, ils meurent. Les conditions changent. Par conséquent, les systèmes persistants doivent apprendre, ce qui nécessite qu'ils modélisent la réalité et minimisent la surprise.

Exemples de modèles : l'acier dans la forge d'un forgeron, le marché, une forêt, une cellule, un arbre, un LLM, le réseau électrique, une entreprise, un service de médias sociaux. En d'autres termes, tout ce qui s'adapte au fil du temps pour anticiper de nouvelles entrées.

À part ça : ces choses ne sont pas seulement des modèles. Elles peuvent aussi être vues sous d'autres angles : un service de médias sociaux est également un ensemble de logiciels, parfaitement fixe et déterministe, traitant des entrées et des sorties. Un humain est un sac lipidique composé principalement d'eau, et aussi une personne, et aussi un modèle.

Les modèles peuvent être considérés comme prédisant une distribution sur des entrées possibles. Un modèle réussi prédit une distribution qui correspond bien à la distribution de ses entrées. Cela signifie qu'il prédit avec précision, exactitude, robustesse et efficacité.

(Ce qui suit est une explication simple du traitement prédictif, du principe de l'énergie libre et de l'inférence active, au cas où vous auriez les connaissances nécessaires).

Nous disons que la distribution prédite est précise lorsqu'elle minimise la divergence par rapport à la distribution d'entrée observée.

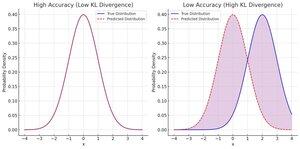
Nous qualifions la distribution prédite de précise lorsqu'elle a une faible variance, ce qui signifie qu'elle fait une prédiction très spécifique. Une prévision plus étroite à une précision donnée ne rapproche pas votre estimation moyenne de l'entrée moyenne, mais elle vous rapproche à chaque estimation !

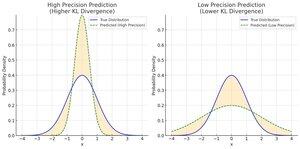
Les prédictions sont robustes au bruit si elles sont aussi simples que possible. Moins un modèle utilise de paramètres et d'interactions entre paramètres pour une prédiction, plus il s'adapte à l'aspect invariant à basse fréquence de l'entrée.

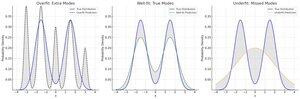
Nous allons principalement passer l'efficacité sous silence ici, mais l'idée principale est que la consommation d'énergie est essentiellement la même que la dépense en bits, que ce soit en précision ou en complexité, il suffit de traduire de la thermodynamique à la théorie de l'information.

Il est facile d'avoir une haute précision de manière vraiment robuste : toujours deviner la même chose. Malheureusement, votre exactitude sera médiocre. En conséquence, nous les considérons généralement ensemble, comme une erreur pondérée par la précision.

Le chemin royal vers une perte pondérée de faible précision a été découvert comme étant la leçon amère : avez-vous essayé plus de paramètres et plus de données ? En fin de compte, vous pouvez surajuster sur l'ensemble des connaissances humaines (LLMs) et c'est plutôt bien. Malheureusement, si le domaine change... ce n'est pas robuste.

Les trois nécessitent un équilibre. Heureusement, vous pouvez tous les marquer en bits. Erreur pondérée par la précision = -log(divergence par rapport aux entrées, pondérée par les précisions) Robustesse alias Complexité = -log(divergence des priors du modèle par rapport à un prior uniforme ou naturel)

Pour toute action ou changement de votre modèle, vous pouvez évaluer combien cela aide en additionnant le bénéfice total en termes de précision, d'exactitude et de robustesse. Cela vaut-il la peine d'ajouter ce paramètre ? Eh bien, les 20 bits supplémentaires de précision compensent-ils les 8 bits de complexité dans vos a priori ?

Lorsqu'on considère un système réel, l'objectif nominal est généralement une certaine forme de précision. Pour l'économie, une forte croissance du PIB et un faible taux de chômage constituent l'"attente préalable" que le système essaie de satisfaire. Pour une entreprise, il s'agit généralement d'une attente préalable de revenus élevés et de faibles coûts.

Bientôt disponible, partie 2 : que se passe-t-il avec nos systèmes ? Comment en sommes-nous arrivés là ? Pourquoi tout devient fou et cassé mais en même temps, tout monte et va vers la droite ?